6. Komplexitätstheorie

Können bestimmte Problemstellungen überhaupt von Computern gelöst werden – und wenn ja, wie effizient?

Komplexität ist ein Maß für die Schwierigkeit eines Problems.

• Zeitkomplexität: Wie lange braucht ein Algoritmhus, um ein Problem zu lösen?
• Platzkomplexität: Wie viel Speicherplatz braucht ein Algorithmus, um ein Problem zu lösen?

Grundlagen: das O-Kalkül / O-Notation / Landau-Symbolik

Die Big-O-Notation wird verwendet, um das Wachstumverhalten einer Funktion zu beschreiben.

Es geht darum zu beschreiben, wie schnell ihre Werte ansteigen, wenn die Eingabe n wächst.

Beispiel: Gegeben sei die Funktion f(n) = 3n² + 5n + 17.

Bei dieser Funktion geht es um die Frage, welcher Teil der Funktion den größten Einfluss auf das Wachstum hat, wenn die Eingabe n sehr groß wird. Der Term 3n²wächst quadratisch, 5n wächst linear und 17 ist ein konstanter Wert (wächst gar nicht).

Für große n wird der Wert von 3n² den der anderen beiden Terme bei weitem übersteigen. Daher ist n² der ausschlaggebende (dominante) Teil für das Wachstum. Die Terme 5n und 17 tragen im Vergleich dazu nur unwesentlich zum Gesamtwachstum bei und werden vernachlässigt.

Auch wichtig ist, dass der konstante Faktor 3 in 3n² irrelevant ist, weil in der Groß-O-Notation nur die Art des Wachstum von Bedeutung ist.

Diese Funktion ist daher in O(n²) (quadratisch). --> f ∈ O(n²) (mit n2 meint man die Menge aller Funktionen die quadratisch anwachsen).

Komplexitätsklassen nach Wachstum (schnell --> langsam):

Komplexitätsklassen

Klassen von Problemen, die mit einer bestimmten Beschränkung von Ressourcen gelöst werden können:

• Ressource = Zeit, Platz
• Beschränkung = polynomiell, exponentiell

Die Schrankenfunktion t(n)

Um die Zeit zu beschränken, definieren wir eine Funktion t(n), die von den natürlichen Zahlen auf die natürlichen Zahlen abbildet (Eingabe und Ausgabe sind natürliche Zahlen). Monoton wachsend bedeutet, dass die Funktion nur ansteigen oder gleich bleiben, aber niemals fallen darf. Das heißt, für eine größere Eingabelänge n ist die erlaubte Zeit t(n) auch größer oder gleich.

Zeitbeschränkte Turing-Maschine

Eine deterministische Turing-Maschine (DTM) heißt t-zeitbeschränkt, wenn sie für jede Eingabe der Länge n nach höchstens t(n) Berechnungsschritten anhält.

Beispiel: Eine Maschine, die für jede Eingabe der Länge n maximal 3n²+5 Schritte benötigt, ist t-zeitbeschränkt für die Funktion t(n)=3n²+5.

Wichtige Prinzipien:

Abhängigkeit von der Eingabelänge n: Die Laufzeit wird immer in Bezug auf die Länge der Eingabe gemessen. Worst-Case-Komplexität: t(n) ist eine obere Schranke. Die Maschine kann schneller fertig sein, aber nie länger brauchen.

DTime

Die Klasse DTIME(t(n)) fasst alle Probleme (Sprachen) zusammen, die von einer deterministischen Turing-Maschine in t(n)-Zeit entschieden werden können.

• D steht für deterministisch.
• TIME steht für Zeit.

Formell ausgedrückt:

DTIME(t(n)) ist die Menge aller Sprachen L, für die es eine t-zeitbeschränkte, deterministische Turing-Maschine gibt, die L entscheidet.

NTime

Die Definition von NTIME beschreibt nicht, wie lange wir brauchen, um das Problem zu lösen, sondern wie lange wir brauchen, um eine vorgeschlagene Lösung zu überprüfen.

• Für jedes x ∈ L existiert ein y ∈ Σ*, sodass χ̂_L(x, y) = a gilt und dieser Funktionswert in O(f(|x|)) viel Zeit berechnet werden kann.

Die Klasse P

Definition:

Die Klasse P beschreibt die Menge aller Entscheidungsprobleme, die von einem deterministischen Algorithmus in polynomialer Zeit gelöst werden können, wobei wir als Modell die deterministische Turingmaschine benutzen. Diese Probleme gelten in der Informatik als effizient lösbar. Diese Algorithmen werden auch als "polynomielle Algorithmen" genannt.

TIME(n^k): Dies ist die Menge aller Probleme, die in einer Zeit von O(nk) gelöst werden können, wobei n die Eingabegröße ist und k eine feste Zahl.

Die Klasse P ist die Vereinigung aller denkbaren polynomialen Zeitklassen. Ein Problem ist also in P, wenn seine Laufzeit durch irgendein Polynom wie n, n2, n100 oder n1000 nach oben beschränkt ist.

Kurz gesagt: Ein Problem ist in P, wenn es einen Algorithmus gibt, der es in polynomialer Zeit löst. Probleme mit exponentieller Laufzeit, wie O(2n), gehören nicht zu P.

info

Die asymptothische Laufzeit beschreibt das Wachstumsverhalten der Laufzeit eines Algorithmus, wenn die Eingabegröße n gegen unendlich strebt. Es geht nicht um die exakte Zeit in Sekunden, sondern um die grundlegende Skalierung des Aufwands. Dafür verwenden wir die Groß-O-Notation.

Man könnten behaupten, dass ein Algorithmus mit einer, nach unserer Definition, effizienten Laufzeit in der Realität beispielsweise 10^100n Schritte benötigen könnten, was praktisch nicht brauchbar (effizient) ist. Allerdings gibt es mehrere Argumente, die solche Fälle ausschließen:

• Es gibt nur sehr wenige bekannte Probleme in P, deren beste Algorithmen eine extrem hohe polynomielle Laufzeit (wie O(n^10)) haben
• Selbst ein langsamer polynomialer Algorithmus stößt bei großen Eingaben sehr viel später an seine Grenzen als ein superpolynomieller (z.B. exponentieller) Algorithmus
• In der Praxis haben sich die Probleme aus der Klasse P als effizient lösbar erwiesen

Probleme mit polynomiellen Algorithmen werden ebenfalls deshalb der Klasse P zugeordnet, weil Polynome unter gängigen Operationen abgeschlossen sind. Wenn mann Polynome addiert, multipliziert erhält man wieder Polynome. Das heißt, wenn man polynomielle Algorithmen kombiniert, bleibt der Gesamtaufwand ebenfalls polynomial. Das macht die Klasse P zu einem robusten und in sich geschlossenen Konzept für "effiziente Lösbarkeit".

Sind reguläre und kontextfreie Sprachen in P?

Reguläre Sprachen sind in P

Für jede reguläre Sprache gibt es einen DEA. Eine Turing-Maschine kann den DEA ganz einfach simulieren, indem sie das Eingabewort der Länge neinmal von links nach rechts liest. Dabei macht die Maschine für jedes Zeichen genau n Schritte (1 Zeichen = 1 Schritt). Das bedeutet, dass der Aufwand der Berechnung direkt proportional zur Länge der Eingabe ist = Lineare Zeit O(n). Da lineare Zeit eine Form von polynomialer Zeit ist, gehören alle regulären Sprachen zur Klasse P.

Kontextfreie Sprachen sind in P

Für kontextfreie Sprachen kann man den CYK-Algorithmus verwenden. Dieser prüft ob ein Wort der Länge n aus den Regeln einer Grammatik in CNF gebildet werden kann. Der Aufwand des CYK-Algorithmus ist kubische Zeit (O(n³)). Da kubische Zeit eine Form von polynomialer Zeit ist, gehören auch alle kontextfreien Sprachen zur Klasse P.

info

Warum ist der Aufwand des CYK-Algorithmus kubisch?

Der Algorithmus füllt eine Tabelle, um zu prüfen, welche Teilwörter der Eingabe von welchen Grammatikregeln erzeugt werden können. Um eine Zelle in dieser Tabelle zu füllen, muss er:

• Alle Längen von Teilwörtern durchgehen (von 1 bis n). → Erste Schleife (O(n))
• Für jede Länge alle möglichen Startpositionen des Teilwortes betrachten. → Zweite Schleife (O(n))
• Für jedes Teilwort alle möglichen Punkte zur Zweiteilung ("Splits") überprüfen. → Dritte Schleife ((n))

Diese drei verschachtelten Durchläufe führen zu einer Gesamtkomplexität von n⋅n⋅n=n3.

Die Klasse NP

In der Klasse NP fassen wir alle Probleme zusammen, für die es einen Algorithmus gibt, der "Lösungen" des Problems effizient verifiziert.

Der Verifizierer

Ein Verifizierer ist ein Algorithmus (Entscheider), der zwei Eingaben erhält: das eigentliche Problem, ein Wort w, und eine Lösung z (Zeuge oder Zertifikat). Die Aufgabe des Verifizierers ist es nicht, eine Lösung zu finden, sondern zu prüfen, ob der Zeuge z ein gültiger Beweis für die Lösbarkeit des Problems ist:

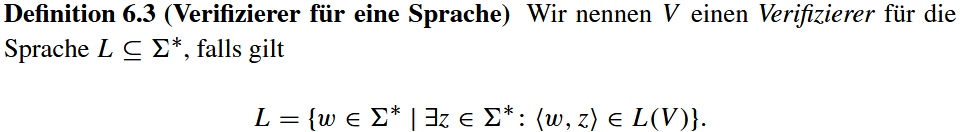
Ein Verifizierer überprüft also, ob ein Wort w aus der Sprache L ist. Für diese Prüfung kann er auf den Zeugen z zurückgreifen. Wenn w ∈ L, muss es einen Zeugen z geben, sodass 〈w, z〉 ∈ L(V ).

Das Hamiltonpfad-Problem als Beispiel

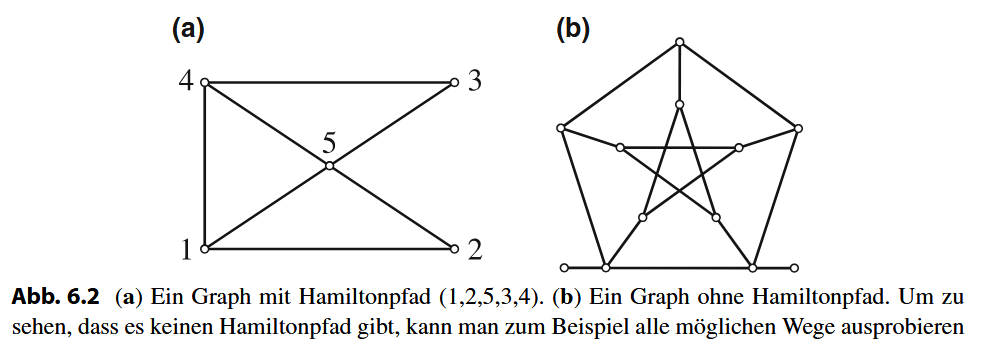
Ein gutes Beispiel ist das Hamiltonpfad-Problem: die Frage, ob es in einem Graphen G einen Weg gibt, der jeden Knoten genau einmal besucht. Dies zu entscheiden kann sehr aufwendig sein. Ein Verifizierer für dieses Problem arbeitet jedoch sehr einfach: Als Zeuge z erhält er eine vorgeschlagene Knotenreihenfolge. Der Verifizierer prüft dann schnell drei Dinge: ob der Zeuge ein gültiger Pfad ist, ob jeder Knoten genau einmal vorkommt und ob alle Schritte im Pfad gültigen Kanten im Graphen entsprechen. Das Überprüfen ist also weitaus einfacher als das Suchen.

Der Verifizierungsalgorithmus garantiert, niemals eine falsche Antwort zu geben: Wenn eine Lösung existiert, gibt es ein Zertifikat, das dies bestätigt; wenn keine existiert, wird kein Zertifikat jemals das Gegenteil beweisen können.

1. Prüfe, ob z syntaktisch die Codierung eines Weges σ ist. Falls nein, stoppe verwerfend.
2. Prüfe, ob σ jeden Knoten des Graphen genau einmal enthält. Falls nein, stoppe verwerfend.
3. Prüfe für jedes Paar (vi , vi+1) von direkt aufeinanderfolgenden Knoten in σ , ob (vi , vi+1) eine Kante in G ist. Falls ja, akzeptiere, ansonsten verwerfe.

Das P vs NP Problem

Das P-vs-NP-Problem ist eine der wichtigsten ungelösten Fragen der Informatik. Die Frage ist, ob jedes Problem, das schnell überprüft werden kann (NP), auch schnell gelöst werden kann (Klasse P).

Jedes Problem, das man in polynomieller Zeit lösen kann (P), kann auch in polynomieller Zeit verifiziert werden (NP), es besteht daher die Beziehung P ⊆ NP. Die große offene Frage ist, ob auch die umgekehrte Beziehung gilt, also ob P = NP ist.

Intuitiv fühlt es sich so an, als wäre das Lösen eines Problems schwieriger als das Überprüfen einer Lösung. So ist es zum Beispiel viel aufwendiger, einen mathematischen Satz zu beweisen, als einen vorgelegten Beweis auf seine Korrektheit zu prüfen. Diese Erfahrung legt nahe, dass P ≠ NP, aber ein formaler Beweis dafür fehlt bis heute. Die Konsequenzen eines Beweises für P = NP wären enorm, da viele moderne Verschlüsselungsmethoden auf der Annahme basieren, dass bestimmte Probleme eben nicht effizient lösbar sind.

NP-Vollständigkeit